エッセイ：大崎 純

研究実施項目

梶原グループによって定式化される離散微分幾何学に基づく変分原理を用い、以下の3つの実施項目を通じて、建築の設計のみならず、構造最適化、応答近似やパラメータ同定で必要とされるさまざまな関数の曲面（多様体）をモデル化するための最適化手法を開発する。具体的な実施項目は以下のとおりである。

1. 区分的連続曲面の幾何学に基づく力学的合理性と「アート性」を備えた曲面の生成法
2. 「美的形状」を有する曲面状建築の設計法
3. 「安全・安心」な建築のための区分的に滑らかな高次元多様体に基づく解析・同定と最適化手法

研究概要

上記１, 2, 3を実現するための具体的な計画は以下の通りである。

1. 合理性とアート性を備えた建築の屋根曲面あるいはファサード（外観）のデザインを生成するには、さまざまな幾何学的および美的形状尺度に基づく区分的に滑らかな曲面の設計法が鍵となる。そのため、CGの分野で実用化されているRicci flowの手法を拡張し、区分的に曲率が一定の曲面、あるいは美的形状尺度や力学的エネルギーなどの幾何的制約条件を近似的に満たす曲面を生成するための効率の良いアルゴリズムを開発することにより、離散微分幾何学における変分原理と不変量に基づく曲面設計法を確立する。また、区分的に滑らかな曲面を美的曲線などの新しい基底曲線で定義して、NURBSに代わる曲面のパラメトリック表現を開発し、「美とアート性」を表現する不変量の定式化が容易な形状モデルを用いた建築曲面の設計法を提案する。
2. 建築の大空間を覆う曲面状の膜構造は、平面の膜から生成され、また、施工後は一様な張力状態が理想的である。そのため、可展面と極小曲面の間の、中間的な曲面が望ましいと考えられる。そのような曲面を設計するため、膜面内の変形量、曲面形状の不変量と自己釣合い状態での張力の関係を導き、変形量を制約して曲面形状を最適化する手法を変分原理に基づき提案する。このような問題は、梶原グループで提案する離散曲面の距離の概念によって多目的最適化問題としての定式化が可能となる。また、剛体折り可能な多面体で形成される建築屋根曲面の形状を離散微分幾何学の不変量を用いて定量化し、可展面に近く剛体折り可能な屋根構造の設計法を提案する。可展面を曲線形状で接続した区分的に滑らかな曲面を、可展面を接続するのではなく、曲面全体の領域における特異点を許容する変分原理により特徴づけ、曲線で分割された区分可展曲面を生成する。これにより、力学的剛性が増し、他の力学的特性の最適化も容易になり、「安全・安心」な「美的形状」の設計が可能となる。
3. 離散微分幾何学の理論を、設計図上での曲面のみならず、構造物に外力が作用した際の変形を表す曲面の近似に拡張し、isogeometric analysisでの新しい基底関数の導入、指定した変形形状を持つ構造の設計、応答分布の不変量と設計の特徴量の関係を用いた類似設計の自動生成などに適用する。また、構造物に荷重が作用したときの応答量を設計変数の関数として予測する問題、あるいは材料試験の結果から構成則を直接的に予測するデータ駆動型の手法では、近似関数は高次元空間内の多様体と考えられる。このような関数を近似するため、従来は滑らかな多様体が用いられてきたが、区分的に滑らかなクラスを許して滑らかさや距離を離散微分幾何学で定式化することで、新しい予測手法を提案し、変分原理に基づく区分的に滑らかな曲面の設計法を一般化する。

研究構想における位置づけ

本研究グループは、建築学と数理工学の研究者で構成され、梶原グループによって提案される離散微分幾何学のさまざまな不変量を用いた形状生成や距離尺度の基礎理論をインプリメントするための手法を開発し建築の設計に適用する。また、区分的に滑らかな曲面を用いた近似曲面により、構造解析や最適化でのさまざまな関数（多様体）の近似精度を格段に向上させる。

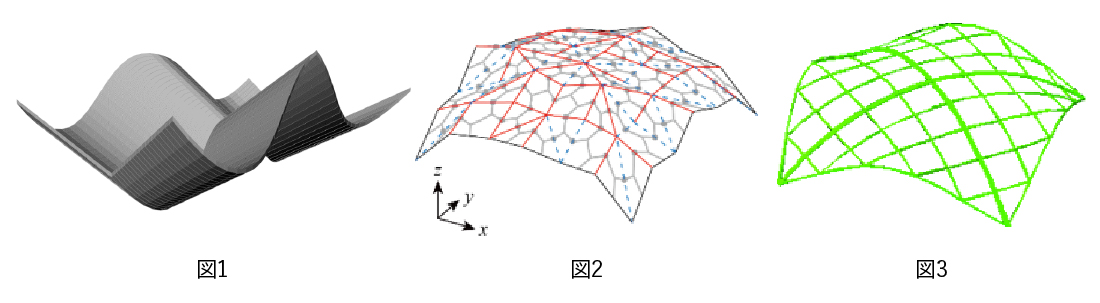
本研究グループでは、これまでに、曲面の滑らかさの指標および幾何的不変量を用いた形状最適化手法を提案した。また、可展面を接続した建築曲面（図1）の最適設計法と、可展面と極小曲面の中間的な曲面による膜構造の設計法を提案した。さらに、剛体折紙を用いた建築曲面（図2）や離散的エラスティカを用いたグリッドシェルの設計法（図3）に関する研究を行っている。これらの研究を拡張して、離散微分幾何学に基づく建築曲面設計の新しい枠組みを構築することは、全体構想を達成するために必要不可欠である。また、最近開始した機械学習の最適設計への応用とデータ駆動型手法による材料構成則の同定に関する研究は、離散微分幾何学の応答予測やパラメータ同定への適用に結び付く研究である。