Research Contents
Miura Group
Research items
- We formulate the curves corresponding to the log-aesthetic curves from the invariants in each Klein geometry such as the Gaussian curvature K=0 for the developable surface and the average curvature H=0 for the minimal surfaces and the membrane structure. We also find the method of deformation preserving the invariants, or the flow equation describing the time evolution by theoretical analysis.
- We implement the method of deformation preserving the invariants as the plug-in of the commercial CAD system (Rhino3D). We study, develop and implement the high-precision and stable algorithm to deform the given plane curve with fixing the endpoints and the directions of the tangents.
- We present the notion of “aesthetic surfaces” based on the Klein geometry and formulate them. We also implement the generation method.
- We restrict the “aesthetic surface” in (3) to the developable surface and the membrane structure to propose “developable aesthetic surface” and “membrane structure aesthetic surface”. Furthermore, we investigate the problems in application to architecture and shipbuilding and their solutions.
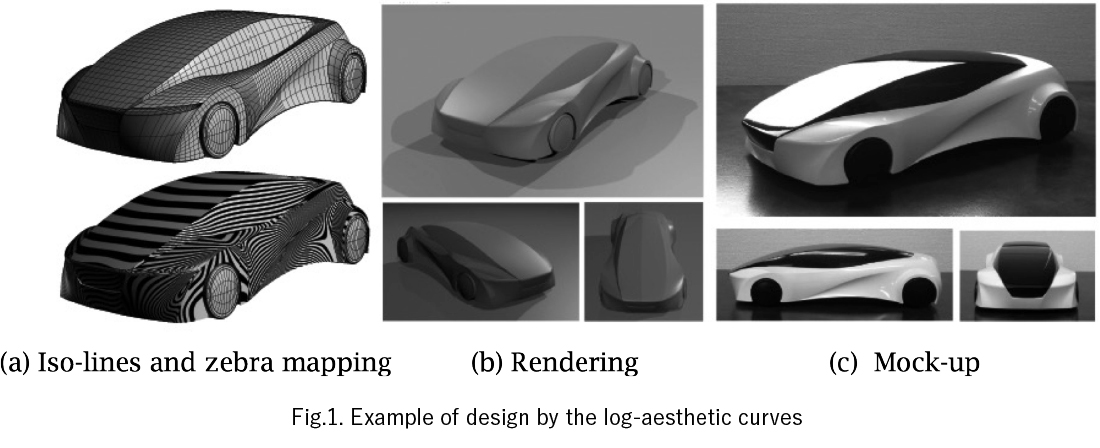
Outline
In design engineering, the B-splines are often used for modeling of the surfaces and curves, but their curvatures drastically change according to the small movement of the control points. In order to overcome this problem, Miura has formulated the “log-aesthetic curves” and proposed the application to the industrial design. Fig. 1 illustrates an example of a design by the log-aesthetic curves. The log-aesthetic curves include the famous curves such as the logarithmic spiral, clothoid, Nielsen spirals, and Miura has implemented as a plug-in of commercial CAD software. However, the expressibility of curves is not yet sufficient for the design of industrial products so that it is not yet spread to practical manufacturing. Also, the mathematical characterization is not clear for the generalization. However, according to our studies, it has been clarified that the essence of the log-aesthetic curves can be captured by the similarity geometry, which is one of the Klein geometries, as shown in Table 1.
In this project, we introduce the theoretical framework of other Klein geometries, extend the log-aesthetic curves further, and create new curves that have not been used in the design engineering. Concretely, we derive the curves corresponding to the log-aesthetic curves in the equi-affine geometry, Möbius geometry, and hyperbolic geometry from the invariants. Then we add the deformation parameter preserving the invariants to derive the flow equation, then we investigate, develop, and implement the deformation. The generalization of the log-aesthetic curves is remaining as an unsolved problem so that we formulate the surfaces available in the design engineering by making use of the theory of Klein geometries.
Placement in the project
The similarity geometry is one of the Klein geometries studying the invariance with respect to the group action of the geometric objects. It is orthodox and classical mathematics, but it has not been well studied without particular remarkable applications. On the other hand, the log-aesthetic curves have been studied in the design engineering based on the Euclid geometry. Still, it has been difficult to capture the essence to generalize them to the space curves and surfaces. From this situation, our research will give an innovative idea and development to three areas, the design engineering, the theory of Klein geometries, and the (discrete) differential geometry. This research aims to introduce the simple, clear, and essential theoretical framework by the Klein geometries, and to construct the curves and surfaces with excellent properties in the design engineering. Our research has a significant meaning in that we solve the mathematical problem in the design engineering by the collaboration of the theory of integrable systems and differential geometry, and that we give innovation to the engineering design by introducing various curves and surfaces which have not been used before.
| Current status | This project |
|---|---|
| LAC has not yet spread to practical use | Add more curves/surfaces for design |
| LAC are characterized by the similarity geometry | New curves based on other Klein geometries |
| No guiding principle for generalizing LAC | Extension by equiaffine, Möbius, hyperbolic geometries |
| No aesthetic surface yet: unavailable for practical use | Surfaces by Klein geometries: application to practical use |
References
- J. Inoguchi, K. Kajiwara, K.T. Miura, M. Sato, W. K. Schief, Y. Shimizu, Log-aesthetic curves as similarity geometric analogue of Euler’s elasticae, Computer Aided Geometric Design (2018).
- K.T. Miura, R.U. Gobithaasan, Aesthetic design with log-aesthetic curves and surfaces, Mathematical Progress in Image Synthesis III, Vol. 24 (Springer, 2016), pp.107-119.
- K.T. Miura, R.U. Gobithaasan, Aesthetic curves and surfaces in computer aided geometric design, International Journal of Automation Technology, Vol.8, No.3, pp. 304-316, 2014.
- K. Kajiwara, T. Kuroda, N. Matsuura, Isogonal deformation of discrete plane curves and discrete Burgers hierarchy, Pac. J. Math. Ind. 8(1) (2016) 1–14.
- J. Inoguchi, K. Kajiwara, K.T. Miura el al., Log-aesthetic curves as similarity geometric analogue of Euler’s elasticae, Computer Aided Geometric Design, Vol.61, pp.1-5, 2018.
- K.T. Miura, S. Suzuki, R.U. Gobithaasan, S. Usuki, A New Log-aesthetic Space Curve Based on Similarity Geometry, CAD and Applications, 16(1), 79-88, 2019.


 Return to Top Page
Return to Top Page